今天來討論最短路徑的另一個演算法，Dijkstra Algorithm。主要內容是指定一個點 (源點) 到其餘各個頂點的最短路徑，也稱作「單源最短路徑」。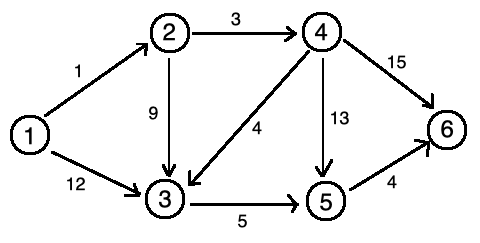

我們用二維陣列 e 來儲存頂點之間邊的關係。

有估計值想必就有「確定值」。那要怎麼做？首先先找出 dis 陣列中離 1 號頂點最近的頂點是 2 號頂點，距離為 1 。所以我們就把 dis[2] 的值變為確定值，代表之後都不會改變。接下來從 2 號延伸，2 號可以走到 3 號和 4 號。

先從 2 → 3 開始。
這時候要比較 2 → 3 的邊能否讓 1 → 3 的路程變短，所以我們現在要比較的是 dis[3] (等於 1 → 3) 和
dis[2] + e[2][3]的大小。

dis[3] = 12, dis[2] + e[2][3] = 1 + 9 = 10, dis[3] > dis[2] + e[2][3]

所以我們把 dis[3] 的值更新為 10。這個動作就叫做「鬆弛」。

同理 2 → 4，我們可以把 dis[4] 的值更新為 4。

dis[4] = ∞, dis[2] + e[2][4] = 1 + 3 = 4, dis[4] > dis[2] + e[2][4]

此時的 dis 陣列為

再來，dis[2]已經找完了，再從剩下的估計值 3、4、5、6 頂點中，找到離 1 號頂點最近的頂點。再透過上面的步驟更新 dis 陣列，直到 dis 陣列中再也沒有估計值為止。

總結一下：

1. 將所有頂點分為兩個部分：已知最短路徑的頂點集合 P 和未知最短路徑的頂點集合 Q。一開始，P 中只有一個源點為已知點，所以用另一個 book[i] 陣列來將源點做記號為 1，表示在 P 之中為已知。若 book[i] = 0 的話表示這個頂點 i 為未知，還在 Q 之中。
2. 設定源點 s 到自己的最短路徑為 0 (dis[s] = 0)。如果 s 能到其他點 i，則把路徑 e[s][i] 存到 dis[i] 之中。若 s 不能到的頂點，路徑 e[s][i] = ∞。
3. 在集合 Q 中找一個頂點 u 離源點 s 最近，將 u 加入到 P 為已知中。並以 u 為起點對其他邊進行鬆弛，比較從 s → u → v 的路徑能否比 s → v 短，可以的話則更新。
4. 重複步驟 3 直到集合 Q 為 0。最終的 dis 陣列就是源點到所有頂點的最短路徑了。

import numpy as np

e = np.zeros((11, 11), dtype=int)
inf = 99999999
key_point = 1

# 讀入頂點個數，邊個數
n, m = map(int, input().split(' '))
# 初始化
for i in range(1, n+1):
    for j in range(1, n+1):
        if i == j : 
            e[i][j] = 0
        else:
            e[i][j] = inf

# 讀入邊
for i in range(1, m+1):
    t1, t2, t3 = map(int, input().split(' '))
    e[t1][t2] = t3

# 初始 dis 陣列，從 key_point 到其餘各點的初始路程
dis = np.zeros(11, dtype=int)
for i in range(1, n+1):
    dis[i] = e[key_point][i]

# 初始 book 陣列
book = np.zeros(11, dtype=int)
book[key_point] = 1

# Dijkstra Algorithm
for i in range(1, n):
    # 找到離 key_point 點最近的頂點
    min = inf
    for j in range(1, n+1):
        if book[j] == 0 and dis[j] < min :
            min = dis[j]
            u = j
    book[u] = 1
    for v in range(1, n+1):
        if e[u][v] < inf:
            if dis[v] > dis[u] + e[u][v]:
                dis[v] = dis[u] + e[u][v]

# 輸出
for i in range(1, n+1):
    print(dis[i])


'''
驗證資料:
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
'''

0 1 8 4 13 17